-

这篇文章除了介绍 Hash算法本身的实现外，还强调了两点知识：

  • Hash算法的目标在于均匀分布
  • 数组使用 2^n 可以加快余数计算

souce:哈希表：散列查找

一、线性查找

我们要通过一个 键key 来查找相应的 值value。有一种最简单的方式，就是将键值对存放在链表里，然后遍历链表来查找是否存在 key，存在则更新键对应的值，不存在则将键值对链接到链表上。

这种链表查找，最坏的时间复杂度为：O(n)，因为可能遍历到链表最后也没找到。

二、散列查找

有一种算法叫散列查找，也称哈希查找，是一种空间换时间的查找算法，依赖的数据结构称为哈希表或散列表：HashTable。

1
2
Hash: 翻译为散列，哈希，主要指压缩映射，它将一个比较大的域空间映射到一个比较小的域空间。
简单的说就是把任意长度的消息压缩到某一固定长度的消息摘要的函数。Hash 算法虽然是一种算法，但更像一种思想，没有一个固定的公式，只要符合这种思想的算法都称 Hash 算法。

散列查找，主要是将键进行 hash 计算得出一个大整数，然后与数组长度进行取余，这样一个比较大的域空间就只会映射到数组的下标范围，利用数组索引快的特征，用空间换时间的思路，使得查找的速度快于线性查找。

首先有一个大数组，每当存一个键值对时，先把键进行哈希，计算出的哈希值是一个整数，使用这个整数对数组长度取余，映射到数组的某个下标，把该键值对存起来，取数据时按同样的步骤进行查找。

有两种方式实现哈希表：线性探测法和拉链法。

三、哈希表：线性探测法

线性探测法实现的哈希表是一个大数组。

首先，哈希表数据结构会初始化 N 个大小的数组，然后存取键 key 时，会求键的哈希值 hash(key)，这是一个整数。然后与数组的大小进行取余：hash(key)%N，将会知道该键值对要存在数组的哪个位置。

如果数组该位置已经被之前的键值对占领了，也就是哈希冲突，那么会偏移加1，探测下个位置是否被占用，如果下个位置为空，那么占位，否则继续探测。查找时，也是查看该位置是否为该键，不是则继续往该位置的下一个位置查找。因为这个步骤是线性的，所以叫线性探测法。

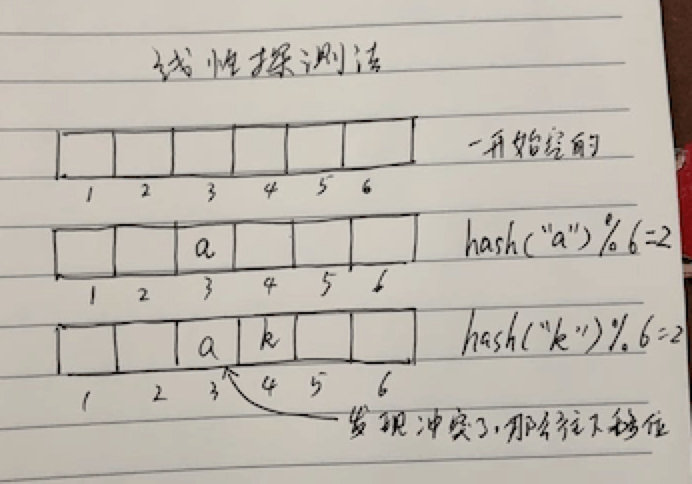
因为线性探测法很少使用，我们接下来主要分析拉链法。

四、哈希表：拉链法

拉链法实现的哈希表是一个数组链表，也就是数组中的元素是链表。数组链表很像一条条拉链，所以又叫拉链法查找。

首先，哈希表数据结构会初始化 N 个大小的数组，然后存取键 key 时，会求键的哈希值 hash(key)，这是一个整数。然后与数组的大小进行取余：hash(key)%N，将会知道该键值对要存在数组的哪个位置。

如果数组该位置已经被之前的键值对占领了，也就是哈希冲突，那么键值对会追加到之前键值对的后面，形成一条链表。

比如键 51 的哈希 hash(51) 假设为 4，那么 hash(51) % 4 = 4 % 4 = 0，所以放在数组的第一个位置，同样键 43 的哈希 hash(43) 假设为 8，那么 hash(43) % 4 = 8 % 4 = 0，同样要放在数组的第一个位置。

因为哈希冲突了，所以键 43 链接在键 51 后面。

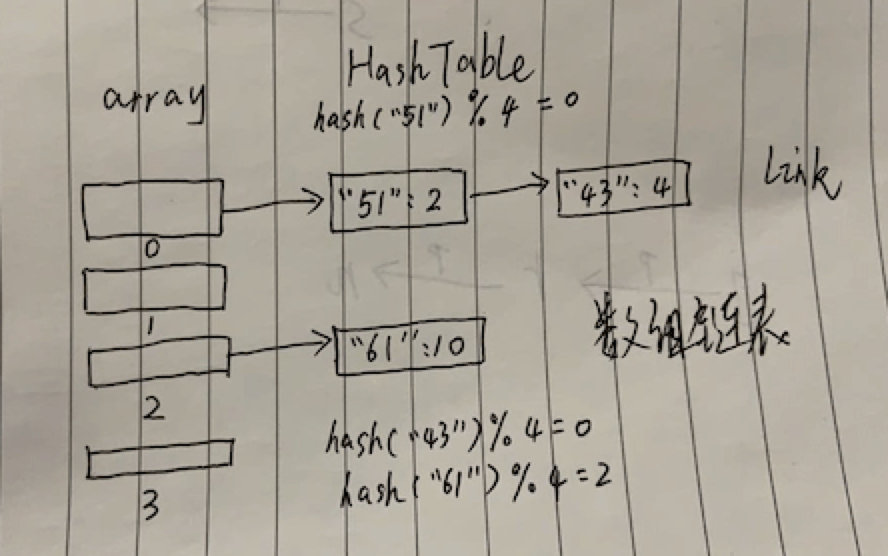
查找的时候，也会继续这个过程，比如查找键 43，进行哈希后得到位置 0， 定位到数组第一位，然后遍历这条链表，先找到键 51，发现不到，往下找，直到找到键 43。

Golang 内置的数据类型：字典 map 就是用拉链法的哈希表实现的，但相对复杂，感兴趣的可参考标准库 runtime 下的 map.go 文件。

五、哈希函数

当哈希冲突不严重的时候，查找某个键，只需要求哈希值，然后取余，定位到数组的某个下标即可，时间复杂度为：O(1)。

当哈希冲突十分严重的时候，每个数组元素对应的链表会越来越长，即使定位到数组的某个下标，也要遍历一条很长很长的链表，就退化为查找链表了，时间复杂度为：O(n)。

所以哈希表首先要解决的问题是寻找相对均匀，具有很好随机分布性的哈希函数 hash()，这样才不会扎堆冲突。

Golang 语言实现的哈希函数参考了以下两种哈希算法：

当然还有其他哈希算法如 MurmurHash: https://code.google.com/p/smhasher 。

还有哈希算法如 Md4 和 Md5 等。

因为研究均匀随机分布的哈希算法，是属于数学专家们的工作，我们在此不展开了。

我们使用号称计算速度最快的哈希 xxhash，我们直接用该库来实现哈希：https://github.com/OneOfOne/xxhash：

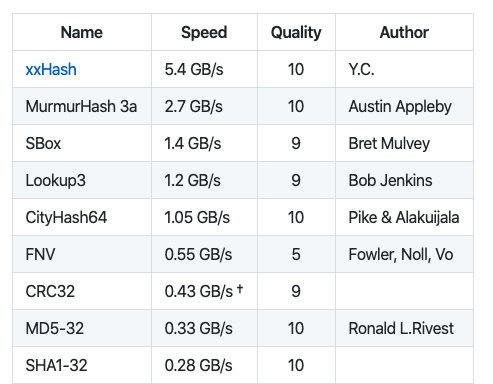
实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
package main

import (
    "fmt"
    "github.com/OneOfOne/xxhash"
)

// 将一个键进行Hash
func XXHash(key []byte) uint64 {
    h := xxhash.New64()
    h.Write(key)
    return h.Sum64()
}

func main() {
    keys := []string{"hi", "my", "friend", "I", "love", "you", "my", "apple"}
    for _, key := range keys {
        fmt.Printf("xxhash('%s')=%d\n", key, XXHash([]byte(key)))
    }
}

输出：

1
2
3
4
5
6
7
8
xxhash('hi')=16899831174130972922
xxhash('my')=13223332975333369668
xxhash('friend')=4642001949237932008
xxhash('I')=12677399051867059349
xxhash('love')=12577149608739438547
xxhash('you')=943396405629834470
xxhash('my')=13223332975333369668
xxhash('apple')=6379808199001010847

拿到哈希值之后，我们要对结果取余，方便定位到数组下标 index。如果数组的长度为 len，那么 index = xxhash(key) % len。

我们已经寻找到了计算较快，且均匀随机分布的哈希算法 xxhash 了，现在就是要解决取余操作中的数组长度选择的问题，数组的长度 len 应该如何选择？

比如数组长度 len=8，那么取余之后可能有这些结果:

1
xxhash(key) % 8 = 0，1，2，3，4，5，6，7

如果我们选择 2^x 作为数组长度有一个很好的优点，就是计算速度变快了，如下是一个恒等式：

1
恒等式 hash % 2^k = hash & (2^k-1)，表示截断二进制的位数，保留后面的 k 位

这样取余 % 操作将变成按位 & 操作：

1
2
3
4
5
6
7
8
9
10
11
12
哈希表数组长度 len=8，
存在一个哈希值 hash=165，二进制表示为 1010 0101

所以： 

165 % 8 
= 165 % 2^3
= 165 & (2^3-1)
= 165 & 7
= 1010 0101 & 0000 0111 
= 0000 0000 0101 
= 5

选择 2^x 长度会使得计算速度更快，但是相当于截断二进制后保留后面的 k 位，如果存在很多哈希值的值很大，位数超过了 k 位，而二进制后 k 位都相同，那么会导致大片哈希冲突。

即使如此，存在很大哈希值的情况很少发生，大部分哈希值的二进制位数都不会超过 k 位，因此编程语言 Golang 使用了这种 2^x 长度作为哈希表的数组长度。

实际上 hash(key) % len 的分布是和 len 有关的，一组均匀分布的 hash(key) 在 len 是素数时才能做到均匀。

1
素数(prime number)，也叫质数，是指在大于 1 的自然数中，除了 1 和它本身以外不再有其他因数的自然数，也就是与任何数的最大公约数都为1。

举例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
f(n)为哈希表的下标，哈希表的长度是 m，而哈希值是 n，记 w=gcd(m,n) 为两个数的最大公约数，

那么：

f(n) = n % m 
     = n - a*m (a=0,1,2,3,4...)
     = w * (n/w-a*m/w)

因为 w=gcd(m,n)，所以 (n/w-a*m/w) 是一个整数。

所以哈希表的下标 f(n) 只会是 w=gcd(m,n) 的倍数，倍数就注定了不会均匀分布在 `[0,m-1]`，除非 w=1。

在哈希值数列数量特别多的情况，对偶数和奇数数列进行取余求下标，如长度 m=5 和 m=6：

哈希数值：2 4 6 8 10 12 14 16 18 20 22...
m=5时下标：2 4 1 3 0 2 4 1 3 0 2...
m=6时下标：2 4 0 2 4 0 2 4 0 2 4...

哈希数值：1 3 5 7 9 11 13 15 17...
m=5时下标：1 3 0 2 4 1 3 0 2...
m=6时下标：1 3 5 1 3 5 1 3 5...

偶数队列可以看到素数5一直重复 `2 4 1 3 0`，而合数6一直重复 `2 4 0`，只有素数均匀分布。

奇数队列可以看到素数5一直重复 `1 3 0 2 4`，而合数6一直重复 `1 3 5`，只有素数均匀分布。

将偶数和奇数数列合并起来，步长为1时，素数和奇数都一样均匀，仅当步长不为1时的随机数列，素数会更均匀点。

我们实现拉链哈希表的时候，为了数组扩容和计算更方便，仍然还是使用 2^x 的数组长度。